In the words of T’Pain, “It’s 5 O’Clock in the morning / Conversation got boring,” and in the words of Neitzsche, “The higher man is distinguished from the lower by his fearlessness and his readiness to challenge misfortune.”
Neither of these ideas are particularly relevant to this blog post. Or, well, the former is relevant to me right now, and the latter is relevant to Valkyrie, I think. If we ever need to define a philosophy, call me at 3:00 AM.
One of the big buzzwords lately on both MVRT and Valkyrie is ‘control theory,’ or to some people, ‘CT.’ And, I hope, most people on this blog know that I’ve been a rather strong advocate of putting more control theory on robots. Well, there’s a method to my madness. Or at least, a reason.
Basically, life is, well, complicated. This can of course be taken as a general truism, but it can also be considered in a different sense. Simply stated, very few things in life are . In fact, most things don’t even have a closed-form solution, which is fancy math-speak for having a solution which can be evaluated before infinity. An example of something without a closed-form solution is (fittingly enough) one of the solutions for the wavefunction of a particle in free space . Not really going to go into that one. Maybe sometime I’ll write about quantum mechanics but only once I’m done being triggered by memories of my Modern Physics class.
Anyway, in between those two rather extreme cases, we have fun little things like , Newton’s 2nd Law, or even more complicated monsters like the Riccati equation (first order, quadratic in the unknown function), which looks like .
What’s a Differential Equation?
We are now going to take a moment to strip the math symbols away. What mathematicians call a ‘differential equation’ is simply an equation which relates two things, and how fast those things are changing (and how fast those things are changing how fast they’re changing, etc). For example, a falling ball is constantly accelerating time passes, going faster and faster each second due to the effects of gravity. However, the faster it goes, the more the wind pushes against it, and the slower it goes.
This is actually a graph of that equation. Essentially, you’re a point in space in the graph, which represents speed in the y-axis and time in the x-axis. At each point, you’re being “pushed” in a direction which is the slope of the solution to the differential equation at that point. What I’m going for here is this: The blue line represents the long-term convergence of the differential equation. As you move through time or speed, you end up at some constant speed no matter how you go. This is the ‘terminal speed’. If I start at 30 m/s and 5s in, at 1,000s I’ll still be at my terminal speed: the blue line. The purple and yellow lines represent what would happen if you started at different velocities. Remember: the y axis is the speed, the x axis is time.
Each little tiny green arrow tells each point where it should be going next.
Voltage Sliders and the Motor Differential Equation
Motors are governed by a relationship I will call the ‘Motor Differential Equation’. It looks like this:
is the angular position, so is the angular velocity and is the angular acceleration. , of course, is the voltage to the motor.
I can’t solve this differential equation, but I did model a motor in Python. This program represents a flywheel spinning. The first graph is a graph of velocity versus time, the second is a graph of voltage versus time.
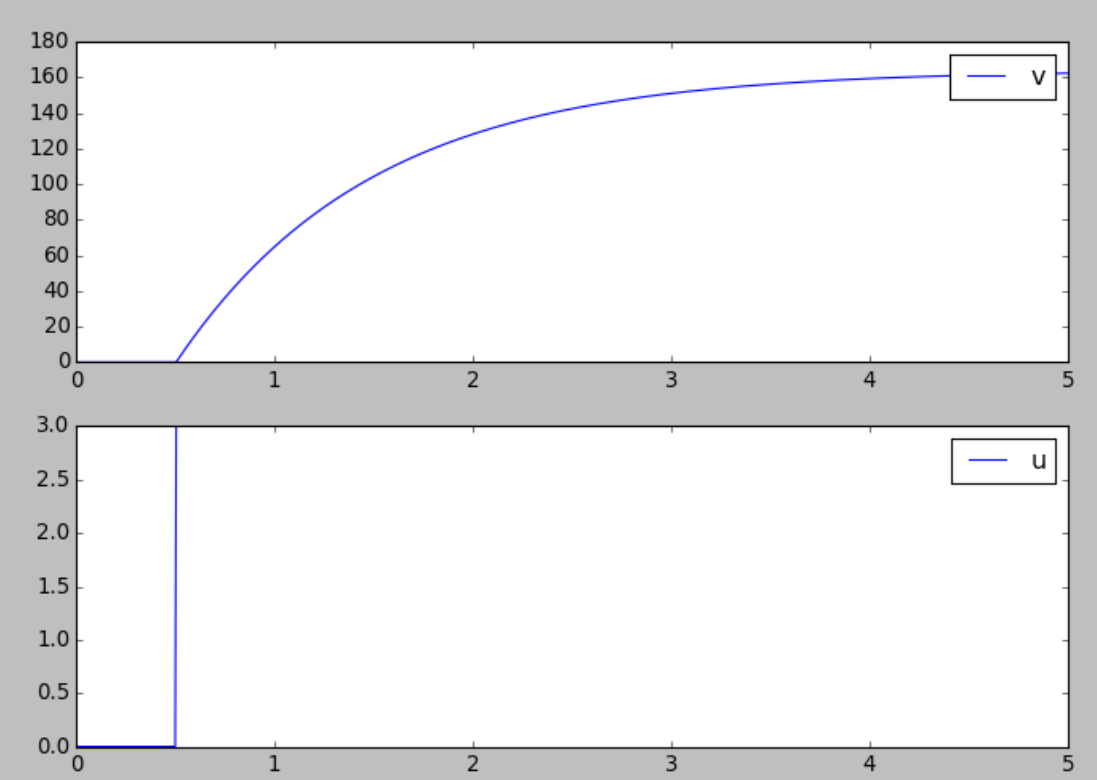
As you can see, it stabilizes around 160 m/s, at around 5 seconds give-or-take, so 4.5 seconds after the input starts. This input represents what would happen if you hooked the motor up to a voltage slider and turned it to 3 V. To record that: 3 V Step Input: 4.5 second spinup
PID and the Motor Differential Equation
Now, let’s put a PID controller on this. If you don’t know what PID is, I’ll have to explain it in a different post.
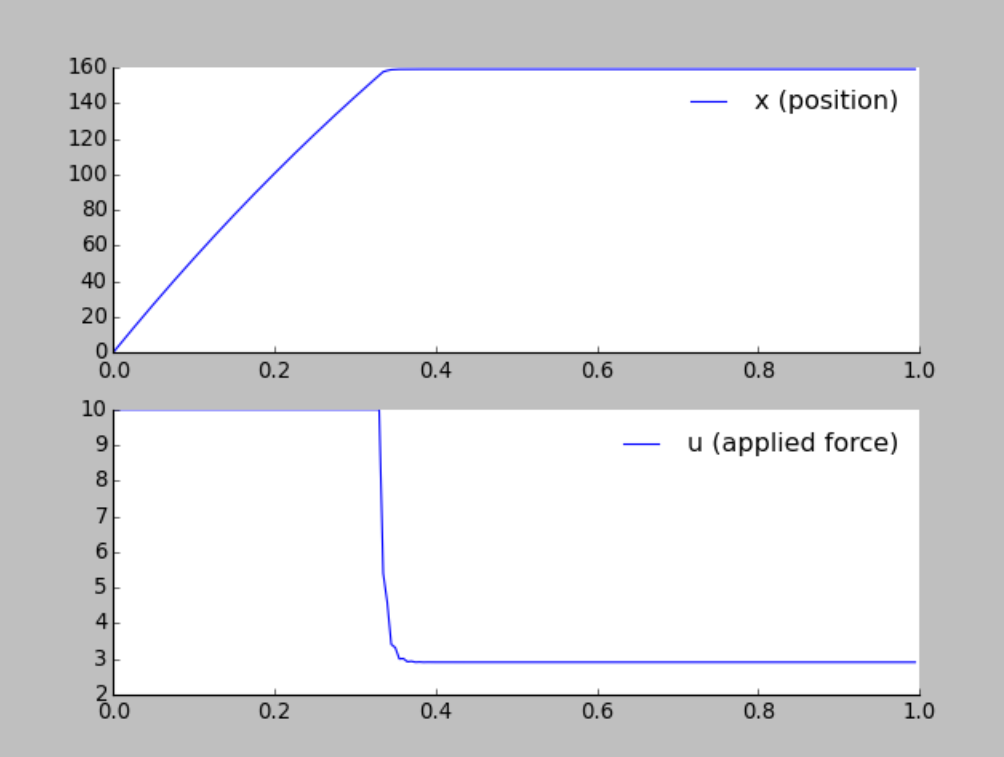
The difference is striking. Settling time is about .28 seconds to spin up to the same speed. Wow. No human could manage this. Here’s how you would do it:
- Max out the voltage slider
- Wait for the motor to get to 160 m/s
- Bring the motor back down to the holding voltage (~2 V)
No only do you not have enough information, you’re not fast enough, and you have no understanding of what the holding voltage is. Furthermore, it’s nearly impossible to intuit. Again, it’s a differential equation without a general-form solution. Intuit that!
More mathematical details in the future.